【Qt】QLineEdit点击调用surface触摸键盘
本文共 403 字,大约阅读时间需要 1 分钟。
surface本身有个触摸键盘,点系统的编辑框就会弹出来,和windows系统里面osk.exe不同。
ui->lineEdit->setEchoMode(QLineEdit::NoEcho);ui->lineEdit_2->setEchoMode(QLineEdit::Password);
设置这两个属性都可以调起触摸键盘。这也是无意中发现的,因为所做的软件有账号密码登录,密码框设置了Password的属性,能自动弹起来,账号框不行,就去看了QLineEdit的源码,想看是怎么调起来的。下面看源码:
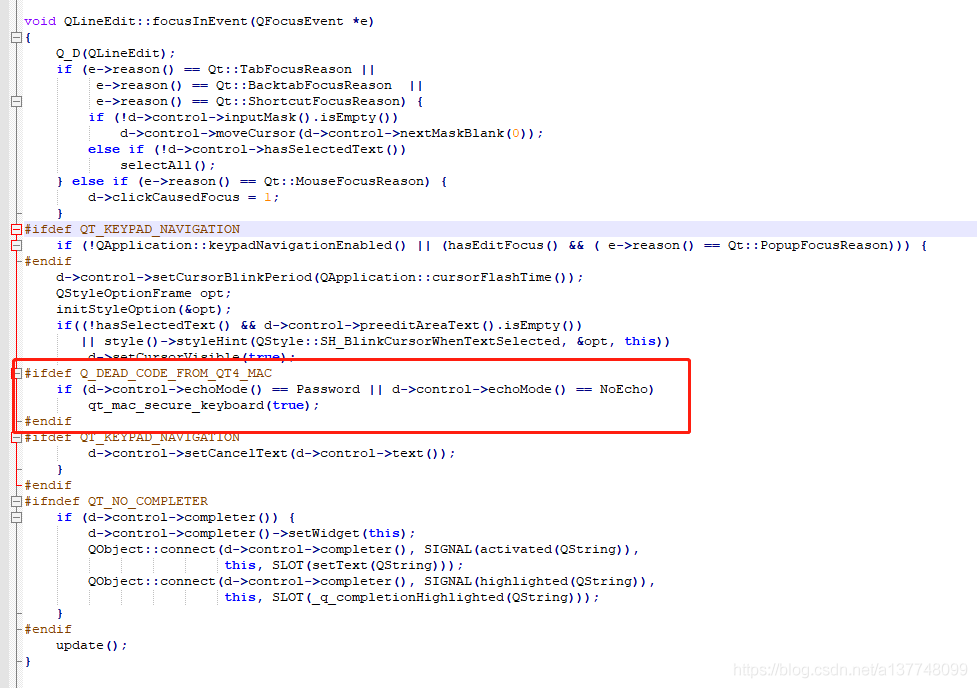
看焦点获取事件,
if (d->control->echoMode() == Password || d->control->echoMode() == NoEcho)
这个判断下面应该就是调起键盘的,网上没搜到qt_mac_secure_keyboard这个是干嘛的,源码也没找到。后续有时间再看
转载地址:http://fiflz.baihongyu.com/
你可能感兴趣的文章